Materi Aljabar Lengkap

Operasi Aljabar

A. Pengertian Aljabar

Bentuk aljabar adalah bentuk bentuk yang mengandung koefisien berupa konstanta dari variabel.

Kofisien yaitu angka yang memiliki variabel (2a,3a,4a,5a,...,).
Konstanta yaitu angka yang tidak memiliki variabel (2,3,4,5...).
Variabel yaitu simbol pengganti angka yang belum di ketahui nilanya, disebut juga peubah (a.b,c,...,z).

Contoh:

2a
(2 disebut koefisien atau angka yang memiliki variabel. a disebut variabel)
3 x -5
(3 disebut Koefisien. x disebut Variabel. 5 disebut Konstanta atau angka yang tidak memiki Variabel).

B. Suku Dalam Aljabar

Dalam operasi aljabar terdapat suatu suku. Suku dalam aljabar adalah jumlah variabel beserta koefisiennya atau konstanta pada aljabar yang dipisahkan oleh operasi jumlah atau selisih
Contoh;

2a Berati satu suku
3x-5 Berati dua suku atau Binom
2x+5y-3 Berati tiga suku atau Trinom
3a+5b-4c+5d-e Berati banyak suku atau Pinom

Suku sejenis yaitu suku yang memiliki variabel yang sama
Contoh:

2x+x-4x
3y-2y+5y

Sedangkan suku tidak sejenis yaitu suku yang memiliki variabel yang berbeda. Contoh:

2x+3y (Tidak sejenis karena variabelnya berbeda)
2 +3x+3x (Tidak sejenis karena 2 hanya konstanta).

Hal yang harus di ingat.
(+)ketemu(+) = (+)
(+)ketemu(-) = (-)
(-)ketemu(-) = (+)
(-)ketemu(+) = (-)
Bila hanya Variabel itu berati angkanya 1 bukan 0

C. Operasi Penjumlahan & Pengurangan Bentuk Aljabar

Syarat untuk operasi penjumlahan & Pengurangan adalah harus satu suku atau variabelnya sama. Contoh:

(5x+3y)+(-3x-10y)

Untuk penyelesaian hal
pertama buka kurungnya.
ke2 pindahkan variabel yang sama atau suku sejenis.
ke3 Hasilkan sesuai dengan suku sejenis.
Dan perhitungan selesi.

5x +3y -3x-10y
= 5x-3x+3y-10y
= 2x-7y
(Cukup samapai sini karena syaratnya kan harus satu suku atau variablenya sama).
(5x+3)-(x-1)
= 5x+3 -x+1
= 5x-x+3+1(Ingat -x bukan berati 0 tapi -1x)
= 4x+4

D. Perkalian & Pembagian Bentuk Aljabar

Di dalam Matematika bila ada angka di depannya dalam kurung artinya di kali
Contoh:

2(3)=6
2(5+2)
(2 X 5)+(2 X 2)
=10+4=14

Bila dalam kurung di depannya dalam kurung artinya di jabarkan.
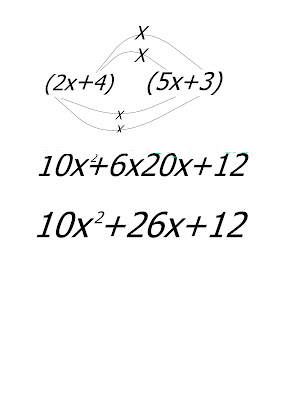
Contoh:

(2+3)(4+1)
(2 X 4)+(2 X 1)+(3 X 4)+(3 X 1)
=8+2+12+3
=25

1. Bentuk umum perkalian dalam aljabar

aXaXa

2a(b+c) = 2ab+2ac
(2a+b) (a+c)
=2a²+2ac+ba+bc
(2a² karena axa=a². Bila sudah belajar pangkat akan mengerti.)
Contoh:
- 5(4x-2y)
  =(5 X 4x)+(5 X -2y)
  =20x-10y
- (Cukup sampai sini karena bila di jabarkan akan menjadi 20xxxxy+12xxxy dan itu beda suku).
- (2p-3q) (5p+2q)
  =(2p X 5p)+(2p X 2p)+(-3q X 5p)+(-3q X 2q)

2. Bentuk Pembagian Dalam Aljabar

Bila perkalian di tambah, pembagian di ambil
.a:a:a

a^m:aⁿ=a^m-n

Contoh

E. Pemfaktoran

Contoh Pemfaktoran berikut :

Sumber gambar google dan tertara

^{Karena awalnya x²} dan semuanya bernilai
positif, jadi pertama bikin 2
kurung yang di dalamnya ada variabel x dan operasi +
1. (x + ?) (x + ?)
  Yang tanda
  tanya itu baru dah diisi dengan
  cara :
2. buat tulisan seperti dibawah ini
  ? + ? =?
  ? X ? =?
3. Isi = yang di tambah dengan
  bilangan koefisien, dan yang
  dikali dengan bilangan
  konsanta
  ? + ? =12
  ? X ? =20
4. Cari bilangan
  berapa + berapa yang hasilnya
  12 dan berapa x berapa yang
  hasilnya 20 dengan syarat atas bawah bilangannya sama.
  Dan bilangannya harus pas dengan hasil yang dijabarkan
  2 + 10 =12
  2 X 10 =20
5. Baru isi kurungnya dengan 2 bilangan atas
  (x +2) (x +10)
  jadi,
  
  = (x +2)(x +10)
1. (x ?) (x ?)
2. ? + ? =-2
  ? X ? =-8
3. -4 + 2 =-2
  -4 X 2 =-8
4. (x -4)(x +2)
  Jadi,
  
  = (x -4)(x +2)
Faktoran seperti ini harus lebih teliti, karena jika salah taruh angka, dan min atau plus salah hasilnya akan berbeda. Caranya hampir sama yang di atas. Jika yang dikali diisi dengan konstanta, sekarang yang dikali diisi dengan konstanta kali variabel kuadrat atau angka pertama, dan ada tambahan langkahnya
1. ? + ? =13
  ? X ?=(5.6)=30
2. 10 + 3=13
  10 X 3=30
3. Ganti koefiesn tidak berpangkat dengan bilang yang dicari tadi
4. faktorkan menjadi 2, seperti faktoran contoh pertama dengan sarat dalam kurungnya sama
  5x(x+2) +3(x+2}
5. Karena dalam kurungnya sama ambil satu kurung saaja, dan buat kurung baru untuk yang di luar
  (5x+3)(x+2)
Pembuktiannya
(5x X x)+(5x X 2)+(3 X x)+(3 X 2)

Jadi, 5x²+13x+6=(5+3)(x+2)
1. ? + ?=-8
  ? X ?=12
2. -6 + -2=-8
  -6 X -2=12
  ingat min kali min jadi plus
4. 3y(y-2) -2(y-2)
5. (3y-2)(y-2)
Pembuktiannya
(3y.y)+(3y.-2)+(-2.y)+(-2.-2)

Jadi, 3y²-8y+4=(3y-2)(y-2)

Saran dari saya agar kalian bisa mengerjakan soal aljabar yaitu:
mengingat operasi bilangan dan syarat penyumlahan dan pengurangan aljabar.
Menurut saya aljabar itu salah satu ilmu dasar matematika. Jadi aljabar harus bisa di kuasai dari sekarang. Jika baru mulai emang akan ada kendala. Tapi kedepannya akan mudah, bila mengetahui intinya. Selanjutnya biar lebih mengerti bisa lihat contoh soal aljabar dan pembahasannya.